Ergo and the Autolykos Consensus Mechanism: Part I

The following is an in-depth, technical breakdown of Ergo’s consensus mechanism, Autolykos. As this is a lengthy and detailed topic, we will publish it in segments over the next two weeks. For Part I, the author starts to break down the block mining pseudocode and guides us through the creation of “list R.”

Part I

Autolykos, the Ergo consensus mechanism, is one of the few asymmetric memory-hard, proof of work puzzles that is still ASIC resistant - thus ensuring that the blockchain is kept as decentralized as possible. Autolykos is based on the Equihash paper[1] and the birthday problem. To summarize, the miner is tasked to find k (=32) out of N elements, such that the hash of the sum of the elements is less than the target. The following pseudocode explains the mining process and this analysis will break down each line extensively since there are very few online resources that explain Autolykos in its entirety.

Autolykos Block Mining Pseudocode

Before discussing the block mining procedure, the algorithm first requires a very large cyclic group G of prime order q with fixed generator g and identity element e. This prime group is used to return integers in Z/qZ during the Blake2b256-based hashing function.

Example cyclic group with generator z, identity element 1, order 6[2]

We will not focus extensively on the cyclic group as it only covers a small segment of the PoW scheme. Now, let’s tackle Autolykos Block mining line by line.

Line 1 – Input h and m

The PoW begins with the two inputs: the block height h and the upcoming block header hash m. The block header hash is a hash of the block header components, such as the previous block header hash, merkle root, nonce, etc.

Line 2 – Calculate list R

Firstly, it is important to notice the H() notation in line 2. This notation calls the hashing function Algorithm 3. Algorithm 3 is a hash function based on Blake2b256 and it is used throughout Autolykos. Algorithm 3 states that if the Blake hash of the inputs is below 2²⁵⁶ (= 16⁶⁴ = 0xFFFFFFFFFFFF86633A9E8F1256D61ED5325EBF2A4B4366BA0000000000000000), then hash.mod(q) is returned. If not, Algorithm 3 repeats until it reaches a numeric hash within the valid range. For reference, note that q is the prime order of group G, Blake2b256 hash outputs are 256 bits, 64 digits long, and Algorithm 3 will always return a numeric hash in Z/qZ.

Blake2b256 Based Hash function

In line 2, the focus is the creation of list R. List R contains r values which are 31-byte numeric hashes created from integers in [0, N). r values are generated by takeright(31,H(j||h||M)). The variables are as follows:

• j, integer in [0, N)
• h, block height
• M, 8kb of constant data - padding to slow down hash calculation

The section takeRight(31,H(…)) means that given H(…), a 32-byte Blake2b256 output, the 31 bytes on the right (i.e. in little endian (whereas other hash algorithms are bit endian)) are returned. In other words, the most significant byte, the byte farthest to the left, is dropped. As a result, each r value is the 31 least significant bytes derived from the 32-byte H(j||h||M)) output. For example, if j = 1, r1 = takeRight(31,H(1||h||M)).List R consists of N elements and can be generated for each block by incrementing j by 1 N-1 times. Since H(…) returns hash.mod(q), we can state that list R consists of r0, 1, 2, 3 … N-1 and list R ⊂ Z/qZ. As stated in the Autolykos v2 whitepaper[3], “N elements are derived from block height and constants, unlike Autolykos v1, so miners can recalculate block candidates easily now (only indexes are depending on them).” In other words, j is always in [0,N), N is determined by h, M is always constant, and h changes every block, the only variable a miner needs to compute list R is h.

List R is stored in RAM. In Autolykos, N = 2²⁶ (67,108,864 integers) is used in implementation for every block before 614400. Thus, the memory requirement for blocks before block 614400 is (226 * 31 bytes =) 2.08GB. N first increased on block 614400. Post block 614400, every 51200 blocks, N increases by 5%. In other words, the memory requirement of an Ergo miner increases by 5% every ~71 days. On block 4198400 the value of N becomes constant and equal 2,143,944,600[4]. Note that the last 2 values listed in the table should be 2,143,944,600 and not 2,147,387,550. After block 4198400, the storage requirement of list R will be (31 bytes * 2,143,944,600) = 66.46GB.

N elements based on block height

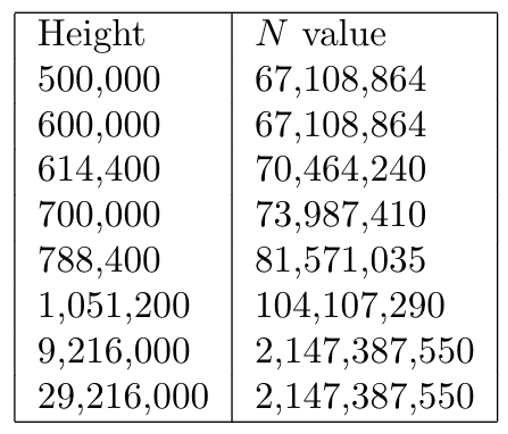
N elements, Ethash vs. Autolykos

Autolykos is like Ethash in the sense that block height determines N elements to be stored in RAM. With Autolykos, block height determines N 31-byte numeric hashes to be stored. With Ethash, block height determines N 128B DAG pages to be stored. You might ask yourself, if an Ergo block occurs every 2 minutes, how are Ergo miners able to generate a 2GB+ dataset so quickly? Ethereum miners only regenerate the DAG every 100 hours because it takes so long… For an Ergo miner, the burden to compute list R is N instances of Algorithm 3; remember, each r value is computed as takeRight(31,H(j||h||M)). However, a GPU can do this very quickly GPUs generally have 32-wide or 64-wide multiprocessors meaning that 32 or 64 Algorithm 3 instances can be done simultaneously depending on the GPU. For example, a 32-wide GPU such as the RTX570 can fill list R in just a few seconds.

For Part II, we will pick up from here and continue the explanation of Autolykos v2. Stay tuned to Ergo’s social media channels for updates on Part II of this series.

[1] https://www.researchgate.net/publication/316904748_Equihash_Asymmetric_Proof-of-Work_Based_on_the_Generalized_Birthday_Problem
[2] https://en.wikipedia.org/wiki/Cyclic_group#/media/File:Cyclic_group.svg
[3] https://www.docdroid.net/mcoitvK/ergopow-pdf
[4] https://www.ergoforum.org/t/autolykos-v-2-details/480
[5] Credit to Wolf9466#9466 on Discord